What Does Beef Look Like After It Starts Crystallization
Equation (3) can be used to calculate the amount of estrus to exist removed from any food sample:
where Q is the heat to exist removed (kJ), ms is the mass of solids in the sample (kg), cp,s and cp,w are the values of specific heat of the solids and water (kJ/(kg·°C)), respectively, λw is the enthalpy of crystallization or fusion of water at the crystallization temperature (kJ/kg), Ti is the initial temperature of the sample to a higher place the crystallization temperature (°C), Tc is the water crystallization temperature (°C), and Tf is the final temperature of the sample beneath the water crystallization temperature (°C). It is important to emphasize that the values of specific heat may not exist constant in a given range of temperatures, and the specific rut of a substance can change with a change in phase [21] [22].
As can exist expected, the presence of solutes in food samples tin can substantially change the crystallization temperature of the water they contain, causing it to have a lower value than the crystallization temperature of pure water. In general, the divergence of the crystallization temperature from that of pure water depends on the blazon of solutes present (their molecular weight) and their concentration [23]. Likewise, the values of specific heat of the solids depend on their specific components and their physical state. Several equations have been reported to predict crystallization temperatures of water in foods, and for calculating specific heat values below and above the corresponding crystallization temperature [24] [25].
Even though it is possible to predict the thermal properties of foods (such as water crystallization temperature and specific oestrus) with empirical equations every bit explained earlier, the realistic amount of full removable heat required to freeze a sample may deviate from the calculated Q value of Equation (three) (which can be seen as a theoretical value or a simplification). Effigy 1 shows the freezing curves of pure water and a food sample. As heat is removed from the food sample, water starts to crystallize at an initial crystallization temperature. At a certain point, the crystallization temperature begins to decrease due to having a more full-bodied solution, and crystallization will come to a stop unless more oestrus is removed from the system. If more heat is removed, 1 or more eutectic temperatures (the temperature at which there is a coexistence of liquid and solid phases) may be reached. After the eutectic temperatures accept been reached, all of the components be in solid class, and the temperature may continue to decrease as more than heat is removed after all the components have undergone crystallization [21].
Figure ane. Temperature history of pure water and a food sample during freezing. Adjusted from Heldman and Singh [21].
iii.2. Heat Transfer and Water Crystallization in Meat
The rate of estrus transfer or freezing rate is influenced by the temperature gradient betwixt the product and the freezing medium, the modes of heat transfer involved (convection, conduction, radiation, or their combination), the shape and size of the production as well every bit its packaging fabric, and the thermal backdrop of the product. The fact that many thermal properties (east.grand., specific heat, thermal electrical conductivity, and enthalpies of phase modify) vary with changes in temperature can make the determination of rates of heat transfer challenging. This, in turn, has created the demand to develop simplified solutions to calculate rates of heat transfer and times required to freeze a production. These solutions usually presume the thermal properties to exist abiding equally a function of temperature [21].
The governing equations of oestrus transfer due to conduction for regular geometries are shown below. Equation (four) corresponds to Cartesian coordinates (rectangular geometries), Equation (v) corresponds to cylindrical coordinates, and Equation (6) applies to a spherical system [26].
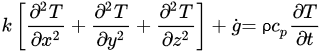 (4)
(4)
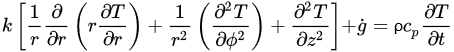 (5)
(5)
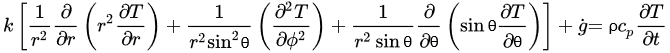 (6)
(6)
Equations (four)–(6) relate the charge per unit of rut transfer in the three dimensions of the respective coordinate systems and the heat generated within thou ˙
(Westward/1000iii), with the change in estrus content in the corresponding working volume (right side of the equations). If a modify in phase (such equally water crystallization during freezing) takes identify, that would demand to exist incorporated in the right side of the equations as the total change in enthalpy. To overcome the lack of accuracy from the apply of empirical models to predict thermal properties and calculate indirect changes in estrus content, thermal analysis seems to be the best arroyo to determine the exact corporeality of rut to be removed to accomplish a divers level of water crystallization. Some of the virtually oft used thermal assay techniques include Differential Scanning Calorimetry (DSC), Differential Thermal Analysis (DTA), and Thermogravimetric Analysis (TG) [27]. Once the total change in enthalpy from a freezing process is adamant through whatsoever of these thermal analysis techniques, it can exist simply taken into account for freezing time calculations. Thermal analyses allow an authentic determination of energy supply or removal requirements [27] [28]. Hobani and Elansari [29] examined the enthalpy modify from –40 to 40 °C of meat through Modulated Differential Scanning Calorimetry (MDSC). These authors were able to decide the heat content (which accounted for the freezing and crystallization of water) every bit a function of moisture, and accurately predicted the changes in specific oestrus along the temperature range studied.
By analytically solving the governing equations to a higher place, it is possible to make up one's mind the rates of heat transfer and temperature distributions in an object, and if it is established that estrus transfer only takes place in i dimension (which in many situations tin can be a condom assumption), those analytical solutions can exist more easily determined. The analytical solutions of the governing equations involve performing the corresponding energy balance in the working volume, applying the known boundary conditions, and solving the differential equation to decide the corresponding integration constants. The belittling solutions are also known as exact solutions since they agree with the boundary weather of the differential equations [30]. An example of a widely used analytical solution for regular geometries is Plank's Equation (Equation (seven)), which tin be used to calculate freezing times assuming that heat transfer is unidimensional [21] [23]:
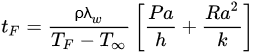
(7)
where tF is the freezing time, ρ is the object's density, TF is the initial freezing bespeak, T ∞ is the cooling medium temperature, a is the characteristic length of the object (the thickness for the example of a slab, or the bore in the case of a cylinder or a sphere), P and R are constants that depend on the object's geometry (slab, cylinder or sphere), h is the convection oestrus transfer coefficient of the cooling medium (which may need to be determined experimentally), and k is the object's thermal conductivity.
Other analytical, semi-analytical, and empirical methods for freezing fourth dimension calculation include a modification of Plank's equation by Cleland and Earle, the method of Lacroix and Castaigne, the method of Pham, the method of Salvadori and Mascheroni, the method of Hung and Thompson, the method of Ilicali and Saglam, the Neumann method, the Tao solutions, the Tien solutions, and the Mott procedure [21] [31]. These methods can be applied to objects with regular shapes (slabs, cylinders, or spheres). Other methods accept been adult that tin can exist applied to predict freezing times of objects with irregular shapes, and include the methods of Cleland and Earle, Cleland et al., Hossain et al., and Lin et al. [31].
The master reward of almost analytical, semi-analytical, and empirical solutions is their simplicity, just they also have limited applicability in real situations. Many of them require the organisation or object being studied to have a regular geometry, which may be very unlikely for biological systems. Additionally, many belittling solutions (such as Plank'due south equation) assume the physical and thermal properties (such equally density, crystallization temperature, thermal electrical conductivity, specific estrus, and enthalpies of crystallization) to be constant, which may be an oversimplification that can crusade substantial deviations from real measurements, and may not take into consideration the changes in enthalpy due to sensible heat in a higher place and below the crystallization temperature. Moreover, belittling solutions assume steady-state heat transfer, a condition that implies that the temperature distribution throughout the system remains constant over time, which is some other ideal scenario rarely found in real situations [21] [xxx]. Additionally, for the specific case of meat and other biomaterials (cellular tissues), the complexity of their construction generates an even greater deviation from the results obtained in analytical solutions, which besides assume samples or objects with a homogeneous mass. This characteristic could simply be expected in a pure substance. In reality, meat samples may exhibit micro-regions or "mushy" regions where crystallization and/or solidification may take place in separated areas, rather than uniformly [26], equally shown in Figure 2.
Figure 2. Unidimensional oestrus transfer and freezing in slabs of pure water and a meat sample. Adjusted from Datta [26].
To overcome the limited accuracy and applicability of analytical solutions, numerical methods can be employed, which involve the sectionalisation of the studied object or medium into small subdivisions that outcome in the aforementioned number of algebraic equations for the unknown temperatures at the nodes located in the interfaces of such subdivisions. These equations can then be solved through computational methods to decide the temperature distributions inside the medium. Some frequently employed numerical methods are the finite difference method, the finite element method, the boundary element method, the finite volume method, and the free energy balance method [30] [32]. These methods tin can exist applied under steady or unsteady state conditions, thereby allowing for the computation of freezing times. The majority of the currently available computational tools and software utilize the finite chemical element method and the finite volume method [32] [33]. Application of numerical methods as well requires the cognition of the initial and purlieus conditions of the process or phenomenon being studied. Some commonly used initial and boundary atmospheric condition include the initial or specified temperature boundary status, the heat flux boundary condition, the convection purlieus condition, the radiations purlieus status, the combined radiation and convection boundary condition, the combined heat flux, radiations and convection boundary condition, and the interface purlieus condition [thirty].
The numerical solutions of the partial differential equations (such equally Equations (4)–(vi)) that draw physical phenomena tin exist used to perform virtual or computational simulations of a variety of processing operations, including freezing. Knowing the necessary energy to be removed from a nutrient sample to reach a specific temperature (and/or the physical and thermal backdrop of the studied food item), as well equally the environmental weather (such equally convective heat transfer coefficients and freezing medium temperature), information technology is possible to predict the time-temperature histories. These predicted values can then be validated in a real experiment, which represents substantial savings in time, material, and labor resource [32].
Lord's day and Zhu [34] conducted computational simulations to determine the freezing time of beef samples with different muscle fiber orientations (parallel to the oestrus transfer direction and perpendicular). In their study, oestrus transfer was assumed to be unidirectional in Cartesian coordinates (Equation (four)), and applied the finite difference method with a Crank–Nicholson formulation. They also took into consideration changes of thermal conductivity with temperature. Overall, their results showed a good fit with the predicted simulation that was utilized. However, other studies took into consideration mass transfer phenomena in their modelling approach, equally water may either condensate or evaporate from the surface of meat samples during freezing or thawing. Delgado and Sun [35] applied the explicit finite difference method to perform simulations of simultaneous heat and mass transfer during thawing of balmy cured ham samples, and the experimental information exhibited a good fit with the partial differential equation applied. More recently, Trujillo and Pham [36] conducted an evaluation of the chilling procedure of a beef carcass through Computational Fluid Dynamics (CFD), which involved simultaneous heat and mass transfer. The tridimensional geometry of the beef carcass was congenital in the software the authors employed through established correlations between the dissimilar parts of the carcass (Figure 3). The authors found that the agreement between the predicted and measured data (such as temperature and superficial moisture loss) depended on the role of the carcass, possibly due to local insulating or mass transfer resistance effects.
Figure 3. Illustration showing an example of the output obtained from the simulation of cooling or freezing through the solution of the heat transfer differential equations through numerical methods. Adjusted from Trujillo and Pham [36].
Source: https://encyclopedia.pub/17224
0 Response to "What Does Beef Look Like After It Starts Crystallization"
Yorum Gönder